这个视频我们来讲解配方法的相关内容,高中数学思想方法大全之一,配方法。
本思想方法涉及以下的模块:函数、导数、数列、不等式、解析几何、三角、向量、概率与统计等。

配方与展开,是代数变形的两种基本方式。
所谓配方法,是一种对代数式进行定向变形的方法,常常配成完全平方,也就是上方等式中N等于2的情况。通过恰当的配凑,使问题明了化、简单化,从而解决数学计算问题的方法。
配方法使用的基本配方依据就是上方的二项式定理。
一般地,一元问题只需一次配方即可;而多元问题常需多次配方。有整体配方、局部配方之分。接下来分别讲解,一元配方问题和多元配方问题。

例1 ,已知函数FX是一个偶函数,若关于fx的不等式恒成立,求不等式中的参数m的最小值。
已知函数FX是一个偶函数,根据偶函数的定义,F(X)=F(-X),代入后,解得α等于1,所以FX等于2的x次方加2的负x次方。
再来看不等式恒成立,注意到F2X的解析式:由FX的解析式,可以得出F2X的解析式,观察式子的结构进行配方,经过配方变形之后,可以变成由FX来表示,FX的平方再减2。
此时不等式变形为M大于等于FX减F2X,也就是M大于等于FX减FX平方加2恒成立。
再对不等式右边进行配方,是一个关于FX的二次函数。由于FX的值域大于等于2,根据二次函数的开口,对称轴。当FX等于2时,取得最大值为0。
M大于等于这个式子恒成立,也就是M大于等于这个式子的最大值。所以得出M大于等于0,所以M的最小值为0。
所以在解题时要关注问题的整体结构,如本题解题的关键点在于:对2X次方加2负X次方这一整体的理解,将其看成一个元。基于对式子的理解只需进行一次配方,问题求解就水到渠成了。配方法结合其他数学知识和性质,有一些常见的配方形式:例如这几种(如图),以及解析几何中的韦达定理和弦长公式等。

例2,若AB满足这个等式,求证A方加B方等于1。
通过观察已知等式的特征,以等式中相加的这两部分,分别为中间项进行配方。
通过配凑,关键在于:这样A方和减A方抵消,B方和减B方抵消。可以得到这个式子(如图)。根据已知等式,那么这个式子正好等于0。也就可以得出这两个平方和为0。
它们都等于0,所以A等于根号1减B方,B等于根号1减A方。两个式子都可以通过两边平方得出A方加B方等于1,得证。
对于有些多元问题,通过观察,分析式子的结构特征,进行配方变形。利用同构关系,构造形如X方加Y方等于0的模型。进而得到X等于Y等于0。
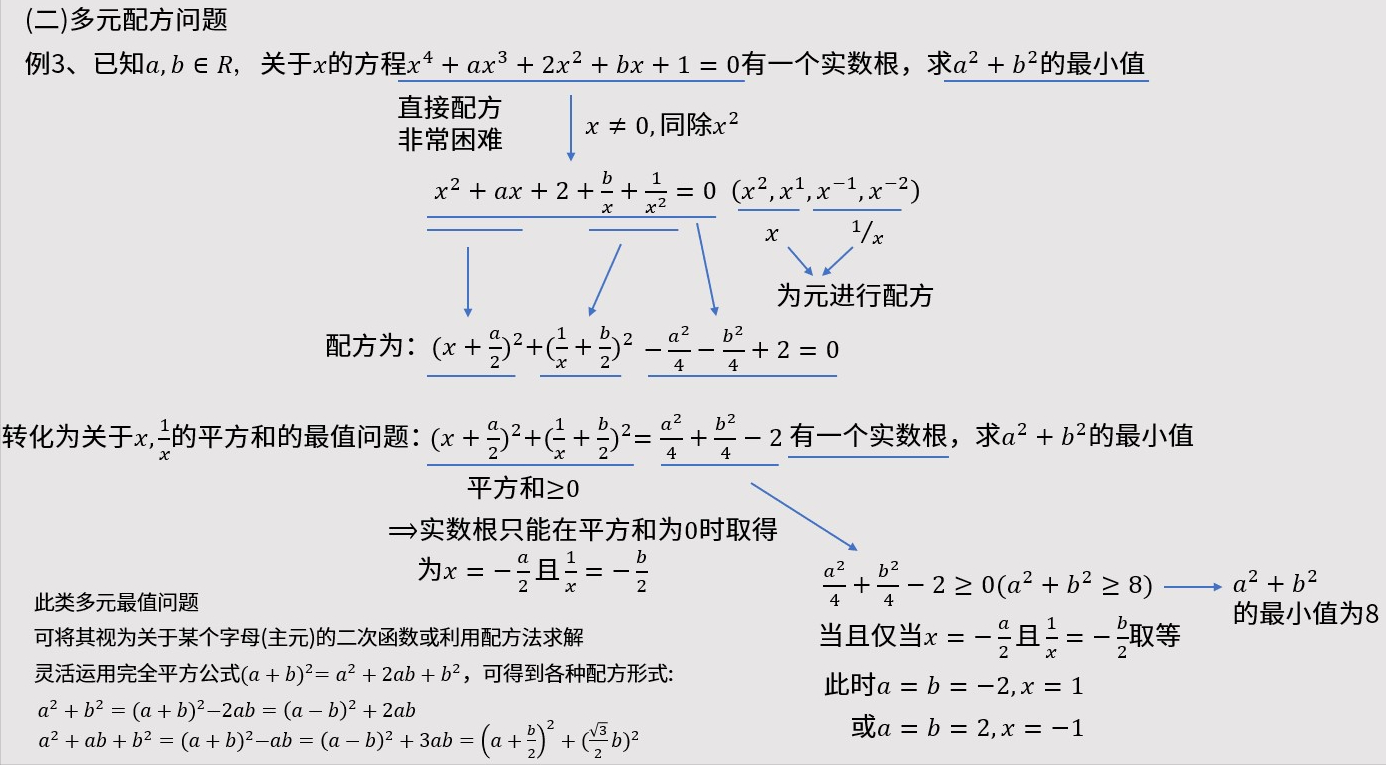
例3、已知参数AB属于R,关于X的方程有一个实数根,求A方加B方的最小值。
本题是以一元方程为背景的最值求解问题。分析题意可知,对于X的四次方程,直接配方非常困难。
可考虑同除X方转化为这样(如图)的等式。X的次方分别为2,1,负1,负2。分别以X,X分之一为元进行配方。配方为X加二分之A的平方,加上X分之1加二分之B的平方。根据已知等式,要再减去4分之A方和4分之B方,再加2才等于0。
把平方以外的都移到等式的另一边。转化为关于X和X分之1的平方和的最值问题,这个方程有一个实数根,求A方加B方的最值。
由于平方和大于等于0, 只有一个实数根,所以这个实数根只能在平方和为0时取得。为X等于二分之A,且X分之1等于二分之B。
等式右边大于等于0,也就是A方加B方等于8。当且仅当X等于负二分之A且X分之1等于负二分之B取等。此时,A等于B等于负2,X等于负1;或A等于B等于2,X等于负1。所以A方加B方最小值为8。
此类多元最值问题,可将其视为关于某个字母的二次函数或利用配方法求解。灵活运用完全平方公式,可得到各种配方形式。
